Characteristics of Indifference Curves (with diagram)
Table of Contents
Characteristics of Indifference Curves
The indifference curves have a number of attributes and interesting properties which have come to be known as characteristic features or properties of indifference curves. The following are some of the important features.
1. Indifference curves slop downward to the right
This is an important and obvious feature of indifference curves. The sloping down indifference curve indicates that when the amount of one commodity in the combination is increased, the amount of the other commodity is reduced. This must be so if the level of satisfaction is to remain constant on the same indifference curve.
Let us consider the logical inferences or conclusions if the indifference curve does not slope downwards from left to right. If it not like that, it should be either parallel to X axis or vertical or it should be an upward sloping curve as shown in the Figure 1.
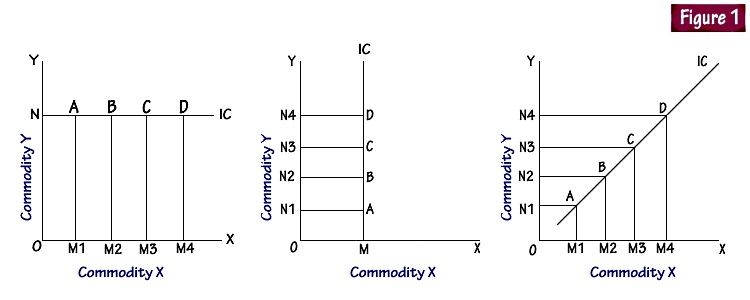
If the indifference curve is horizontal to X axis, the various points on the curve A,B,C,D denoting various combinations of x commodity and y commodity may not have equal significance. At point B, the consumer gets more of x than at point A and at point C, the consumer gets still more of x while the quantity of y remains constant.
As the consumer moves along the indifference curve he is getting a fixed quantity of y but increasing quantities of x. So the consumer cannot be indifferent, as having rational behavior, he would prefer D more than C, C more than B and B more than A and the level of satisfaction is not the same. Each succeeding combination is better than the previous one. Therefore an indifference curve cannot be horizontal since different combinations on the curve differ in significance.
Similarly, an indifference curve cannot be vertical as shown in the figure, as in point D, the consumer gets more of y commodity than at point C, B or A while the x commodity remains constant; so the consumer cannot be indifferent to various combinations as they denote different satisfactions.
In the upward sloping curve too, the different points on the curve differ in significance because as he moves from point A to B, he gets more of x and more of y commodities. So, he cannot be indifferent to the combinations. Similarly point C is better than point B and D is better than point C as the combinations differ giving the consumer greater satisfaction.
Only in a downward sloping curve the loss in one is compensated by the gain in another commodity so that the different points on the curve will be of equal significance and satisfaction to the consumer and he may be indifferent to the various combinations. So, a horizontal or vertical or sloping up curve is not possible.
2. Every indifference curve to the right represents a higher level of satisfaction
Every indifference curve to the right of the preceding curve indicates higher level of satisfaction and the curve to the left shows lesser satisfaction. This means that the indifference curve at a higher level from the axes shows greater satisfaction than an indifference curve at a lower level. This can be illustrated by having two indifference curves as given in Figure 2.
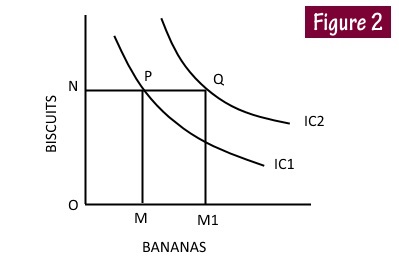
In the indifference curve IC1 at point P the consumer is having OM quantity of Bananas and ON quantity of Biscuits. At point Q in the IC2, the consumer though having the same quantity of Biscuits, the quantity of Bananas has increased from OM to OM1, i.e., at point Q the consumer gets larger quantities than at point P and naturally position Q is preferred by the consumer than position P as in the former he gets larger satisfaction due to larger commodities.
An indifference curve on the right is preferred than the indifference curve on the left. The consumer will always try to move up in the indifference map so that he can occupy as much as possible the topmost curve, as higher curves give larger satisfaction in the difference map.
3. Indifference curves cannot intersect each other
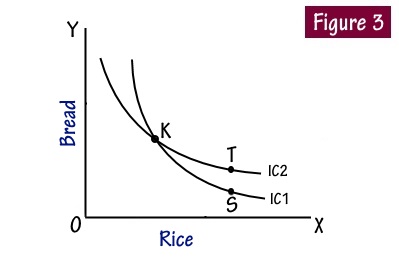
The indifference curves never cut each other as higher and lower curves show different levels of satisfaction. Suppose two indifferent curves cut each other at point K as shown in Figure 3. This means that points K and T which are on the same indifference curve IC2 show equal satisfaction; similarly points K and S which are on the same indifference curve IC1 show equal satisfaction.
K = T, K = S, therefore, S = T
Since K is common to both the curves, points S and T show equal satisfaction. But this is contrary to our earlier assumption that points on a higher indifference curve show greater satisfaction than points on lower indifference curves. In order, therefore, to be consistent with our assumptions; different indifference curves would not cut each other.
4. Indifference curve will not touch the axis
Another characteristic feature of indifference curve is that it will not touch the X axis or Y axis. This is born out of our assumption that the consumer is considering different combinations of two commodities.
If an indifference curve touches the Y axis at a point P as shown in the figure, it means that the consumer is satisfied with OP units of y commodity and zero units of x commodity. This is contrary to our assumption that the consumer wants both commodities although in a smaller or larger quantities. Therefore the indifference curve will not touch either the X axis or Y axis.
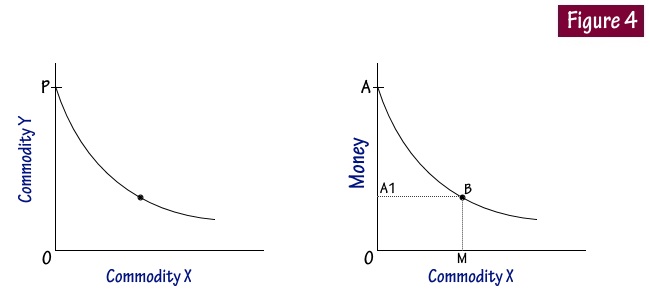
But as a special case it will touch the Y axis at point A if the combination is between Money and Commodity as shown in the Figure 4. It would then mean that the consumer either wants various combinations of money and commodity or only OA units of money which gives him command over commodity X. At point B in the figure the consumer has OM units of commodity X and OA1 units of money and this gives him the same satisfaction of having only OA units of money which means command over x and other commodities.
5. Indifference curves are convex to the origin
The very important feature of the indifference curves is that they are convex to the origin and they cannot be concave to the origin. A normal indifference curve will be convex to the origin and it cannot be concave. Only convex curves will lend to the principles of Diminishing Marginal Rate of substitution. In the case of concave curve, it will lead to increasing marginal rate of substitution which is impossible.
In order to understand this more clearly we have to study the exact purport and significance in passing from one point to another on an indifference curve which is convex to the origin.
In the Figure 5, the indifference curve is convex to the origin. The consumer passes from point A to B on the same curve to remain in the same level of satisfaction. While moving from A to B the consumer gives up YY1 or AC units of Y commodity in order to obtain XX1 units of X commodities, i.e., CB units of X.
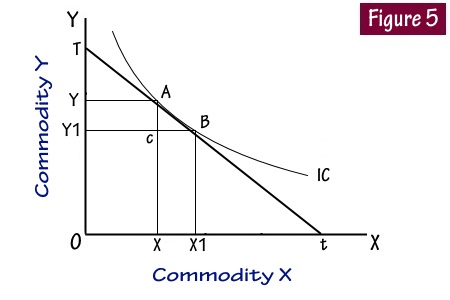
According to the figure, CB units of x give the same satisfaction or utility as AC units of y. This means
CB units of x = AC units of y
1 unit of x = (AC / CB) units of y
This means that one unit of x gives the same satisfaction or utility as (AC/CB) units of Y. In other words, the Marginal Significance of x = (AC/CB) units of y. In the triangle ACB, AC/CB = Perpendicular/Base = the tangent of angle ABC.
Assumption:
The points A and B on the indifference curve are so close to each other that they almost fall on the same straight line Tt which is touching the indifference curve.
In the figure, since angle ABC is equal to angle TtO, the marginal significance of x in terms of y is given by the tangent of the angle TtO. As the points A and B are assumed to lie so near, the same tangent can pass through both of them. The marginal significance of x in terms of y is shown by the angle which the tangent makes on the X axis. So, Marginal Significance of x = Tangent of the angle TtO.
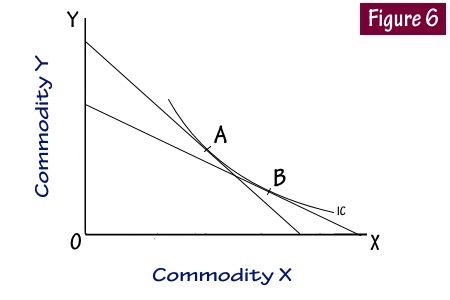
As the consumer moves down an indifference curve taking more of x commodities, the marginal significance of x declines in terms of y commodities. As the marginal significance of x declines, the tangent of the angle TtO should also decline as both are directly related in the figure. This is possible only if the curve is convex.
In the Figure 6, the tangent at point A makes a bigger angle on the X axis than the tangent at point B which makes a smaller angle. This shows that the marginal significance of x in terms of y is declining as the consumer travels down an indifference curve and has more units of x.
It is the declining significance of x and increasing significance of y as the consumer travels down an indifference curve which makes its shape convex to the origin and this forms the basis of Prof. Hick’s Diminishing marginal rate of substitution. On the contrary we shall see what would be the result if the curve is concave.
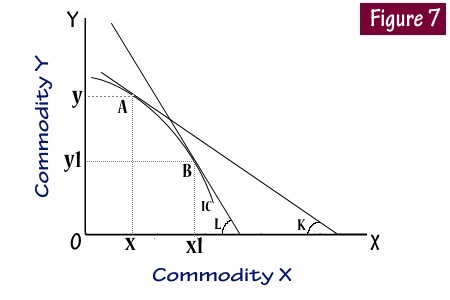
In the figure 7, the indifference curve is concave to the origin. At point A of the indifference curve the consumer has ox units of x and oy units of y when the marginal significance of x in terms of y is given by the tangent of the angle AKO. Now the consumer travels down the indifference curve and comes to point B where he has ox1 units of x and oy1 units of y. The marginal significance of x in terms of y at this new point is given by the tangent of the angle BLO. Since angle BLO is greater than the angle AKO, it follows that the marginal significance of x is greater at point ‘B’ on the curve and the marginal significance of x is smaller at point A on the curve.
This gives the conclusion that as the consumer travels down the indifference curve, the marginal significance of x has become greater as the respective angles of tangents are greater. This is wrong and against the fundamentals of economics and consumption.
The marginal significance of x cannot be greater if the consumer travels dawn the curve enabling him to possess more of x commodities. The marginal significance of x should become smaller and smaller as he possesses larger and larger quantities of x. Since a concave curve violates the fundamental principle of economics, the indifference curve cannot be concave. Only convex curve is in tune with the principles of economics. So indifference curve is convex to the origin.


